Number of Ways to Reorder Array to Get Same BST
Given an array nums that represents a permutation of integers from 1 to n. We are going to construct a binary search tree (BST) by inserting the elements of nums in order into an initially empty BST. Find the number of different ways to reorder nums so that the constructed BST is identical to that formed from the original array nums.
For example, given nums = [2,1,3], we will have 2 as the root, 1 as a left child, and 3 as a right child. The array [2,3,1] also yields the same BST but [3,2,1] yields a different BST.
Return the number of ways to reorder nums such that the BST formed is identical to the original BST formed from nums.
Since the answer may be very large, return it modulo 10^9 + 7.
Example 1:
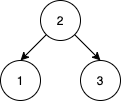
Input: nums = [2,1,3] Output: 1 Explanation: We can reorder nums to be [2,3,1] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.
Example 2:
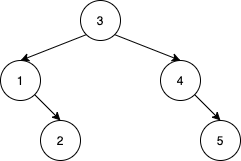
Input: nums = [3,4,5,1,2] Output: 5 Explanation: The following 5 arrays will yield the same BST: [3,1,2,4,5] [3,1,4,2,5] [3,1,4,5,2] [3,4,1,2,5] [3,4,1,5,2]
Example 3:
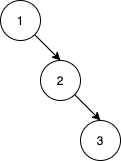
Input: nums = [1,2,3] Output: 0 Explanation: There are no other orderings of nums that will yield the same BST.
Example 4:
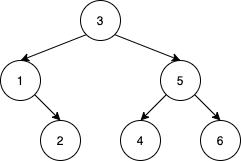
Input: nums = [3,1,2,5,4,6] Output: 19
Example 5:
Input: nums = [9,4,2,1,3,6,5,7,8,14,11,10,12,13,16,15,17,18] Output: 216212978 Explanation: The number of ways to reorder nums to get the same BST is 3216212999. Taking this number modulo 10^9 + 7 gives 216212978.
Constraints:
1 <= nums.length <= 10001 <= nums[i] <= nums.length- All integers in
numsare distinct.
class Solution {
public:
int numOfWays(vector<int>& nums)
{
long long int mod=1e9+7;
int n=nums.size();
table.resize(n+1);
for(int i=0;i<=n;++i)
{
table[i]=vector<long long> (i+1,1);
for(int j=1;j<i;++j)
{
table[i][j]=(table[i-1][j-1]+table[i-1][j])%mod;
}
}
long long ans=dfs(nums,mod);
return ans % mod - 1;
}
private:
vector<vector<long long>> table;
long long dfs(vector<int> nums,long long int mod)
{
int n=nums.size();
if(n <= 2) return 1;
vector<int> left,right;
for(int i=1;i<n;++i)
{
if(nums[i]<nums[0])
left.push_back(nums[i]);
else
right.push_back(nums[i]);
}
long long int right_res=dfs(right,mod)%mod;
return ((((table[n-1][left.size()]%mod)*left_res)%mod)*right_res)%mod;
}
};
---------------------------------------------------------------------------------
----------------------------------------------------------------------------------
This is actually a mathematical problem that can be solved by combination calculation,what'd you do is basically arranging left and right sub-trees in correct order but in all possible combinations.
For example for array [3,6,4,1]
[3,6,4,1] left subtree is [1], right tree is [6,4],
we just need to keep 6 appear in front of 4 to make permutation a valid one,
so combinations can be [6,4,1], [6,1,4], [1,6,4]
Obviously, if left subtree length is 1 and the total length is 3, the combination is 3C1 which is 3
Expand to a more complicated case [3,6,4,1,7]
left sub tree is [1], right tree is [6,4,7],
permutations for right tree itself is [6,4,7], [6,7,4] which means it's 2C1 (combination of [4]
and [7])
for every permuration of right tree you can also combine it with left tree [1] so total # is
4C1*2C1=8
Tseudo code:
def dfs(nums):
if len(nums) <= 2:
return 1
left = [x in nums which < nums[0]]
right = [x in nums which > nums[0]]
return combination(len(lefft+right), len(left)) * dfs(left) * dfs(right)
Here comes the tricky part for Java, doing mathematical stuff in Java is really a PAIN in the ass
since it doesn't have comb() function in python and it doesn't support long long, I didn't know
why the hint is dynamic programming, now I get it, I can use Yang Hui/Pascal's triangle to speed
up calculation and get rid of overflow, are you serious leetcode?
class Solution {
private static final long MOD = 1000000007;
public int numOfWays(int[] nums) {
int len = nums.length;
List<Integer> arr = new ArrayList<>();
for (int n : nums) {
arr.add(n);
}
return (int)getCombs(arr, getTriangle(len + 1)) - 1;
}
private long getCombs(List<Integer> nums, long[][] combs) {
if (nums.size() <= 2) {
return 1;
}
int root = nums.get(0);
List<Integer> left = new ArrayList<>();
List<Integer> right = new ArrayList<>();
for (int n : nums) {
if (n < root) {
left.add(n);
} else if (n > root) {
right.add(n);
}
}
// mod every number to avoid overflow
return (combs[left.size() + right.size()][left.size()] * (getCombs(left, combs) % MOD) % MOD)
* getCombs(right, combs) % MOD;
}
private long[][] getTriangle(int n) {
// Yang Hui (Pascle) triangle
// 4C2 = triangle[4][2] = 6
long[][] triangle = new long[n][n];
for (int i = 0; i < n; i++) {
triangle[i][0] = triangle[i][i] = 1;
}
for (int i = 2; i < n; i++) {
for (int j = 1; j < i; j++) {
triangle[i][j] = (triangle[i - 1][j] + triangle[i - 1][j - 1]) % MOD;
}
}
return triangle;
}
}
---------------------------------------------------------------------------------





