Given an incomplete Sudoku configuration in terms of a 9 x 9 2-D square matrix (mat[][]). The task to print a solved Sudoku. For simplicity, you may assume that there will be only one unique solution.

Given an incomplete Sudoku configuration in terms of a 9 x 9  2-D square matrix (mat[][]). The task to print a solved Sudoku. For simplicity, you may assume that there will be only one unique solution.

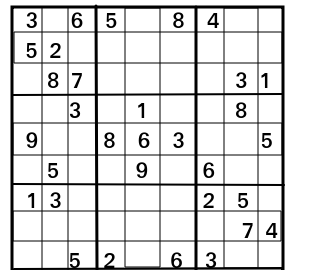
Example:

Input:

1

3 0 6 5 0 8 4 0 0

5 2 0 0 0 0 0 0 0

0 8 7 0 0 0 0 3 1

0 0 3 0 1 0 0 8 0

9 0 0 8 6 3 0 0 5

0 5 0 0 9 0 6 0 0

1 3 0 0 0 0 2 5 0

0 0 0 0 0 0 0 7 4

0 0 5 2 0 6 3 0 0

Output:

3 1 6 5 7 8 4 9 2 5 2 9 1 3 4 7 6 8 4 8 7 6 2 9 5 3 1 2 6 3 4 1 5 9 8 7 9 7 4 8 6 3 1 2 5 8 5 1 7 9 2 6 4 3 1 3 8 9 4 7 2 5 6 6 9 2 3 5 1 8 7 4 7 4 5 2 8 6 3 1 9

#include <iostream>

using namespace std;

#define N 9

int a[N][N];

bool safe(int i,int j,int l)

{

// checking value in  row and column correspond to indexes i,j;

// if l found in any row or column then return false

    for(int k=0;k<N;++k)

    {

        if(a[i][k]==l||a[k][j]==l)

        return false;

    }

// finding rs and cs for checking l in 3x3 matrix

    int rs=i-i%3;// initial row position from where 3X3 start

    int cs=j-j%3;// initial col position from where 3x3 start

//if l is found in 3x3 matrix then return false

    for(int h=0;h<3;++h)

    {

        for(int p=0;p<3;++p)

        {

            if(a[h+rs][p+cs]==l)

            return false;

        }

    }

// all possibillty checked for safe then return true

    return true;

}

bool solve()

{

    int flag=0,i,j;

    for( i=0;i<N;++i)

    {

        flag=0;

        for( j=0;j<N;++j)

        {

            if(a[i][j]==0)

            {

            flag=1;

            break;

            }

        }

        if(flag)break;

    }

//if i and j both is N then return true

    if(i==N&&j==N)

    return true;

// checking possible value from 1 to 9 to suitable for that position

    for(int k=1;k<=N;++k)

    {

        if(safe(i,j,k))

        {

            a[i][j]=k;

            if(solve()) // here is backtracting condition  if false go to previous 

position check another possibility 

             return true;

             a[i][j]=0;

        }

    }

    return false;

}

void printsudo()

{

    for(int i=0;i<N;++i)

    {

        for(int j=0;j<N;++j)

        {

         cout<<a[i][j]<<" ";

        }

    }

}

int main() {

//code

int t;

cin>>t;

while(t--)

{

   //int a[N][N];

   for(int i=0;i<N;++i)

   {

       for(int j=0;j<N;++j)

       {

           cin>>a[i][j];

       }

   }

   

  if(solve())

  printsudo();

  cout<<endl;

    

}

return 0;

}